Ähnlich wie die Unterscheidung von Gleich-, Wechsel- und Drehstrom ist auch der Unterschied zwischen Scheinleistung, Blindleistung und Wirkleistung nicht ganz intuitiv. Wer sich aber mit dem Thema Ladeeffizienz beschäftigen möchte, kommt um ein grundlegendes Verständnis dieser Begriffe nicht herum. Im Folgenden beschreibe ich, was man an einer Steckdose messen kann, wenn verschiedene Verbraucher angeschlossen sind¹. Die Grafiken unten sind mit einer kleinen Computersimulation errechnet, sie sind quasi der “Idealzustand”. Abgesehen von Messungenauigkeiten wird man in der Realität aber zu den gleichen Ergebnissen kommen.

Ohmscher Verbraucher

Stellen Sie sich einen Wasserkocher vor. Dieser besteht im Wesentlichen aus Kabeln, einem Schalter und einem Heizdraht. Der Wasserkocher wird in eine normale Schuko-Steckdose gesteckt, arbeitet also mit einer Nenn(-wechsel-)spannung $U$ von 230 Volt. Der Nennstrom $I$ beträgt 10 Ampere. Man kann nun recht einfach die effektive Scheinleistung $S$ausrechnen:

$$ S = U_{eff} \cdot I_{eff} = 230V \cdot 10A = 2300 VA$$

Das ist allerdings nur eine Betrachtung des Durchschnitts. Der reale Wert schwankt ja mit dem Netzsinus, also mit etwa 50 Hertz. Für viele Anwendungen ist dieser Durchschnittswert vollkommen ausreichend. Aber, Sie ahnen es: Um die Blindleistung zu verstehen, müssen wir tiefer einsteigen.

Wer sich an meine Erklärung des Wechselstroms erinnert kann sich auch ganz einfach vorstellen, wie Spannung und Strom aussehen, wenn man diese über die Zeit misst:

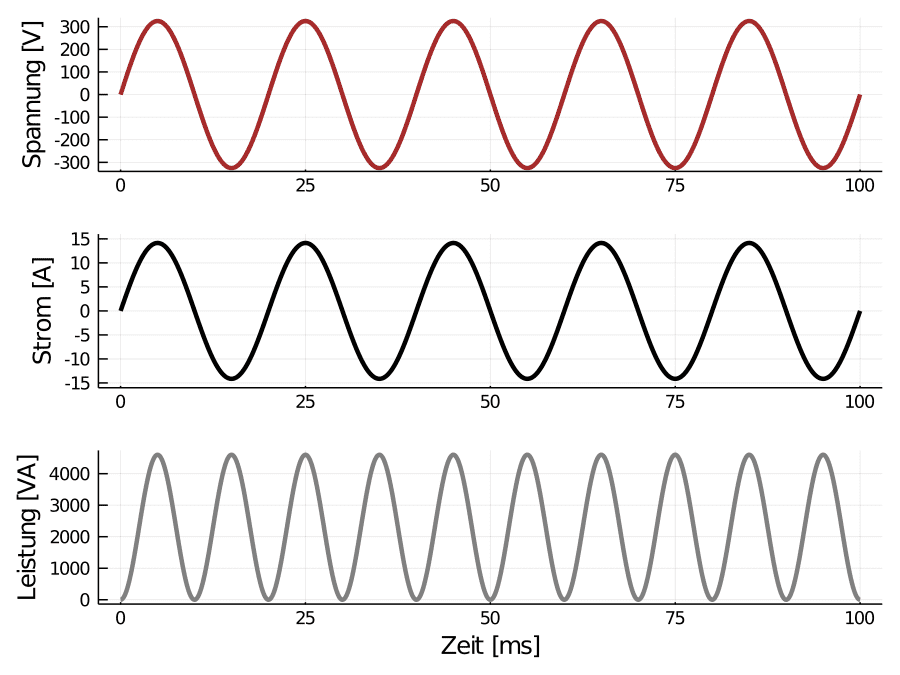
Sowohl Spannung als auch Strom schwanken zwischen ihren Spitzenwerten². Der Graph oben zeigt ja Spannung und Strom im Millisekundenbereich. Man kann nun jeweils die Spannungs- und Strommesswerte zum gleichen Zeitpunkt miteinander multiplizieren. Das Ergebnis ist die dritte Kurve darunter. Diese entspricht der Momentanleistung $p$: Sie schwankt genauso wie der Strom und die Spannung. Aus der Momentanleistung wiederum kann man die Wirkleistung $P$ ableiten:

$$ P = \overline{p} = \overline{u \cdot i} = 2300 W$$

Große Buchstaben nutzt man in der Elektrotechnik, um Durchschnittswerte über die Zeit darzustellen. Kleine Buchstaben sind hingegen Momentanwerte zu einem bestimmten Zeitpunkt. Die Formel oben kann man also wie folgt lesen: “Die Wirkleistung P entspricht der durchschnittlichen Momentanleistung, die wiederum dem durchschnittlichen Produkt aus Momentanspannung und Momentanstrom entspricht.”

Die Leistung ist in diesem Fall komplett positiv, sprich: Die ganze Leistung wird als Wirkleistung genutzt. Das ist typisch für einen ohmschen Verbraucher: Der Wasserkocher in obigem Beispiel hat weder eine Spule (induktiv) noch einen Kondensator (kapazitiv). Beide Bauteile verändern, wie sich der Strom im Verhältnis zur Spannung ändert, und diese beiden Bauteile verursachen Blindleistung ³. Da sie hier nicht vorhanden sind, entsteht auch keine Blindleistung.

Induktive Geräte

Anders verhält sich ein induktiver Verbraucher wie ein Elektromotor. Gleiche Spannung ($U_{eff}=230 V$), gleicher Strom ($I_{eff}=10 A$), also auch gleiche Scheinleistung ($S=2300 VA$). Trotzdem verändert sich die Werte:

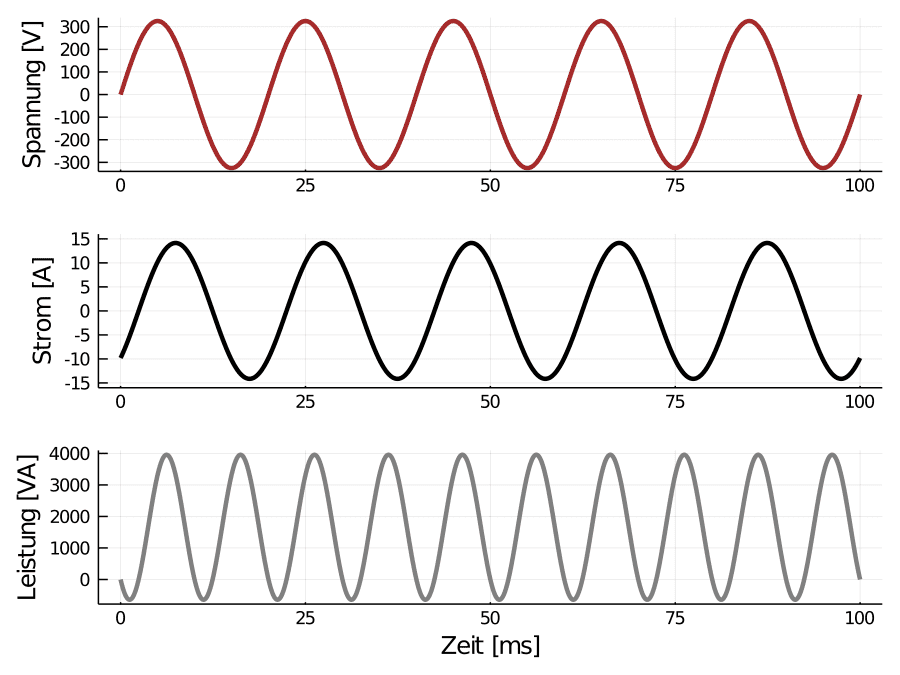
Auf den ersten Blick sieht der Graph zwar gleich aus, aber das ist nur bei der Spannung der Fall. Der Strom ist zeitlich verschoben: Während oben Spannung und Strom gleichzeitig wechselten, läuft hier der Strom der Spannung hinterher. Die Stromkurve startet nicht — wie oben — bei null, sondern bei -10 Ampere. Daher verändert sich auch die Wirkleistung:

$$ P = \overline{p} = \overline{u \cdot i} = 1655,9 W$$

Die Wirkleistung $P$ ist also sehr viel geringer als die Scheinleistung $S$ (2300 VA). Das kann man auch schon anhand der Kurve sehen: Der Durchschnitt der Leistungskurve liegt niedriger, den die Leistung im Graph hat auch negative Werte.

Hier passiert Folgendes: Der Elektromotor besteht nur aus einer Spule. Diese wird, wenn man Wechselstrom anschließt, abwechselnd ge- und entladen. Damit baut man ein Magnetfeld auf, das im Takt des Wechselstroms seine Orientierung ändert. Das Magnetfeld schließlich wird dazu genutzt, um den Strom in eine mechanische Bewegung umzuwandeln.

Die Physik der Spule bewirkt allerdings auch, das die Spule den Strom in Relation zur Spannung etwas verzögert aufnimmt. Wenn zu Beginn die Spannung steigt, dauert es eine Weile, bis der Strom ebenso steigt. Dann kehrt sich das ganze um: Die Spannung sinkt, und mit einer gewissen Verzögerung folgt der Strom wieder. Oder auch: Der Strom läuft der Spannung hinterher.

Für die Leistung bedeutet dies: Es kann — im Gegensatz zum ohmschen Verbraucher oben — auch eine negative Leistung geben. Bildlich gesprochen zieht der Motor also Leistung aus dem Stromnetz, das entspricht den positiven Leistungswerten. Aber: Er speist auch Leistung zurück ins Netz ein, nämlich genau dann, wenn die Leistungswerte oben negativ sind. Es gibt also einen gewissen Anteil an Strom, der nichts weiter tut, als in den Motor rein- und wieder raus zu fließen. Er pendelt quasi, und trägt nichts zur eigentlichen Arbeit des Motors bei.

Sie ahnen es vielleicht schon: Die Leistung, die hier hin- und herpendelt, ist genau die Blindleistung. Die Wirkleistung trägt zur Wirkung des Motors bei — die Blindleistung nicht. In diesem Beispiel ist die gesamte Blindleistung $Q_{tot}$ sogar relativ hoch:

$$ Q_{tot} = \sqrt{S^2 - P^2} = 1594,6 var$$

Wer diese Zahl nun etwas komisch findet: Machen Sie nicht den Fehler, einfach Wirk- und Blindleistung zu addieren, um die Scheinleistung zu berechnen ($1655,9 W + 1594,6 var \neq 2300 VA$)⁴. Den Vergleich der Leistungsarten anhand eines Bierglases findet man zwar oft im Netz, es ist streng genommen aber falsch. Die korrekte Gegenprobe für die Scheinleistung wäre⁵:

$$ S = \sqrt{P^2 + Q_{tot}^2} = 2298,8 VA $$

Blindleistung

Die Blindleistung ist also der Leistungsanteil, der nichts zur Wirkung des Gerätes beiträgt und einfach vor- und zurückpendelt. Das führt auch dazu, das die Blindleistung nicht abgerechnet wird: Der Stromzähler läuft mit positiven Leistungswerten quasi vorwärts und mit negativen rückwärts. Deshalb müssen Sie lediglich die Wirkleistung bezahlen⁶.

Allerdings muss auch die Blindleistung erzeugt werden. Eine Stromleitung selbst braucht sogar einen gewissen Blindleistungsanteil, damit sie überhaupt Wirkleistung übertragen kann. Deshalb wird in der Elektrizitätswirtschaft oft nur mit Scheinleistungen gerechnet, da sie beide Arten von Leistung berücksichtigt. Es gibt auch Grenzen für die Erzeugung von Blindleistung, weshalb in vielen Industriebetrieben Kompensationsanlagen für Blindleistung eingesetzt werden. Diese verhindern, dass große Verbraucher mit entsprechend hoher Blindleistung ins Stromnetz rückwirken können.

Außerdem gibt es neben der oben beschriebenen “Verschiebungsblindleistung” auch die “Verzerrungsblindleistung”. Diese ist mittlerweile auch das wichtigere Phänomen. Die Abweichung zwischen Spannungs- und Stromkurve kommt hier nicht durch eine zeitliche Verschiebung, sondern durch Verzerrung der Stromkurve zustande. Diese ist dann keine ideale Sinuskurve mehr, sondern etwas verzerrt. Diese Verzerrung kommt durch die angeschlossenen Geräte zustande. Vor allem Schaltnetzteile führen zu Verzerrungen, und da fast in jedem Gerät ein Schaltnetzteil steckt, ist der ideale Netzsinus fast nirgendwo mehr anzutreffen. In der Wirkung sind Verschiebungs- und Verzerrungsblindleistung allerdings gleich.

Hier gibt es keine Werbung, denn ich schätze meine Unabhängigkeit. Ich schreibe diese Texte nicht, um reich zu werden — aber ich mag Kaffee. Wenn Ihnen der Text also eine Kleinigkeit wert ist: Hier geht es zu meiner Kaffeekasse, vielen Dank!